様々なオートエンコーダによる異常検知

こんにちは。sinyです。

最近ディープラーニングのオートエンコーダの学習をしていて、いろいろな種類のオートエンコーダがあることを知ったためmnistデータを使っていろいろと試してみました。

オートエンコーダとは？

オートエンコーダ（AutoEncoder)とは、入力と出力が同じになるようにニューラルネットワークを学習させるような手法です。

オートエンコーダについては、以前以下の記事で解説していますので参考にしてみてください。

ディープラーニングで簡単な時系列データの異常検知

2019.2.3

こんにちは。sinyです。 昨年G検定に合格してからも、少しずつですがディープラーニングの勉強も継続しています。 業務経験ゼロなので偉そうなことは全く言えないのですが、最近受講したディープラーニングを用いた異常検知セミナーの知識を使って、実際に業務に生かせる領域がないかちょっとだけ探ってみましたので...

ディープラーニングにおけるオートエンコーダの種類

ディープラーニングにおけるオートエンコーダといっても、ネットワークの構成によって様々な種類がありますが、今回は以下の5つの手法をご紹介します。

なお、今回試したサンプルコードはJupyterNotebook形式で以下のGithubにUPしてあります。

https://github.com/sinjorjob/auto_encorder_test

Undercomplete Autoencoder

まず最初は、Undercomplete Autoencoder(不完全なオートエンコーダ)というものですが、これは一般的に説明されているオートエンコーダのことです。

中間層の次元が入力の次元よりも小さくなるようなものをUndercomplete Autoencoderと呼んでいます。

データロードと前処理

from keras.datasets import mnist
from keras.layers import Input, Dense
from keras.models import Model
import numpy as np

(x_train, _), (x_test, _) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.

x_train 、x_testはそれぞれ(60000, 28, 28) 、(10000, 28, 28)次元のデータになります。

kerasのInput形状に合わせるために入力の形状を(データ数, 28, 28)⇒(データ数, 784) に変形します。

x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))

x_train 、x_testはそれぞれ(60000, 784) (10000, 784) 次元のデータになります。

Kerasによるモデルの定義

モデルの定義は以下の通りです。

encoding_dim = 32
input_img = Input(shape=(784,))
encoded = Dense(encoding_dim, activation='relu')(input_img)
decoded = Dense(784, activation='sigmoid')(encoded)
autoencoder = Model(input=input_img, output=decoded)

autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')

入力層(784次元）→中間層（32ユニット、relu)→出力層(784次元、sigmoid)という単純な3階層のオートエンコーダモデルです。

学習

kerasのfitメソッドを使って学習を行います。
学習データとテストデータに同じx_trainを与えることで入力と同じデータを出力させるように学習させていきます。

autoencoder.fit(x_train, x_train,
                nb_epoch=50,
                batch_size=256,
                shuffle=True,
                validation_data=(x_test, x_test))

入力画像と出力画像を可視化

最後に入力と出力画像を可視化してみます。

import matplotlib.pyplot as plt

# テスト画像を変換
decoded_imgs = autoencoder.predict(x_test)
print(decoded_imgs.shape)

# 何個表示するか
# plt.subplot(行数, 列数, 何番目のプロットか)
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
    # オリジナルのテスト画像を表示
    ax = plt.subplot(2, n, i+1)
    plt.imshow(x_test[i].reshape(28, 28))
    plt.gray()
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)

    # 変換された画像を表示
    ax = plt.subplot(2, n, i+1+n)
    plt.imshow(decoded_imgs[i].reshape(28, 28))
    plt.gray()
    ax.get_xaxis().set_visible(False)  #軸の値の表示を無効化
    ax.get_yaxis().set_visible(False)  #軸の値の表示を無効化
plt.show()

上が入力データ、下が出力データです。
若干薄れている部分がありますが、大体は再現できていることが確認できますね。

Sparse Autoencoder

Sparse Autoencoderは中間層のユニット数が入力層より多いネットワーク構造をしたオートエンコーダです。
中間層に対してペナルティ関数（L1,L2など）を与えることで中間層のユニットの値の大部分を０(情報を伝えない）にすることで過学習を抑える効果があります。

モデルの定義と学習

データの前処理はUndercomplete Autoencoderのケースと同様なので省略します。

モデル定義は以下の通りです。

中間層の定義「activity_regularizer=regularizers.l1(l1))(input_img)」でL1正規化の制約を加えている点が違う点です。

from keras import regularizers

encoding_dim = 32　# 隠れ層のユニット数
l1 =1e-6　# L1正則化のパラメータ
input_img = Input(shape=(784,))

# activity regularizerを加える
encoded = Dense(encoding_dim, activation='relu',
                activity_regularizer=regularizers.l1(l1))(input_img)
decoded = Dense(784, activation='sigmoid')(encoded)
autoencoder = Model(input=input_img, output=decoded)


autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')

autoencoder.fit(x_train, x_train,
                nb_epoch=50,
                batch_size=256,
                shuffle=True,
                validation_data=(x_test, x_test))

以下の図が学習結果です。

若干薄れている部分がありますが、Sparse Autoencoderでも大体は復元できていることが確認できました。

Sparse Autoencoders場合は指定する正規化パラメータの値によって精度がものすごく変わってくるので最適なパラメータ値を選定することが重要になってくると思います。

以下、3パターンで実験した結果です。

Deep Autoencoder

これまでみてきたAutoencoderはエンコーダ、デコーダの部分だけを考えると中間層が存在しませんが、ここを多層にしたものがDeep Autoencoderです。

データの前処理や学習方法についてはこれまでと全く同様なので省略します。

モデルの定義

入力（784次元）⇒エンコーダ（128⇒64⇒32）→デコーダ（64⇒128⇒784）という形状の多層（ディープ）にした形のネットワーク構成になっています。

encoding_dim = 32
input_img = Input(shape=(784,))

encoded = Dense(128, activation='relu')(input_img)
encoded = Dense(64, activation='relu')(encoded)
encoded = Dense(32, activation='relu')(encoded)

decoded = Dense(64, activation='relu')(encoded)
decoded = Dense(128, activation='relu')(decoded)
decoded = Dense(784, activation='sigmoid')(decoded)

autoencoder = Model(input=input_img, output=decoded)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')

autoencoder.fit(x_train, x_train,
                nb_epoch=100,
                batch_size=256,
                shuffle=True,
                validation_data=(x_test, x_test))

以下が学習結果です。

だいぶ鮮明に復元できていることが確認できました。

Convolutional Autoencoder

Convolutional Autoencoderはその名の通りAutoencoderでCNNを使うことにより学習させようというモデルです。

前処理

mnistからロードしたデータをkerasのConv2DモデルのInput形状に合わせるため以下の形状に変形しておきます。

x_train ：　(60000, 28, 28) 　⇒　(60000, 28, 28, 1)
x_test ：　 (10000, 28, 28)　 ⇒　(10000, 28, 28, 1)

from keras.layers import Input, Dense, Conv2D, MaxPooling2D, UpSampling2D
from keras.models import Model
from keras.datasets import mnist
import numpy as np

(x_train, _), (x_test, _) = mnist.load_data()

x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.

print(x_train.shape)
print(x_test.shape)
x_train = np.reshape(x_train, (len(x_train), 28, 28,1))
x_test = np.reshape(x_test, (len(x_test), 28, 28,1))
print(x_train.shape)
print(x_test.shape)

モデルの定義

モデルはエンコーダ部分に畳み込み3回とMaxPooling3回、デコーダ部分に畳み込み4回と
Upsampling3回で最後にシグモイド関数を指定しています。

形状は、入力が(28,28,1)、最終的な出力も(28,28,1)になるようなネットワークモデルになっています。

input_img = Input(shape=(28, 28, 1))

x = Conv2D(16, (3, 3), activation='relu', padding='same')(input_img)
x = MaxPooling2D((2, 2), padding='same')(x)
x = Conv2D(8, (3, 3), activation='relu', padding='same')(x)
x = MaxPooling2D((2, 2), padding='same')(x)
x = Conv2D(8, (3, 3), activation='relu', padding='same')(x)
encoded = MaxPooling2D((2, 2), padding='same')(x)

x = Conv2D(8, (3, 3), activation='relu', padding='same')(encoded)
x = UpSampling2D((2, 2))(x)
x = Conv2D(8, (3, 3), activation='relu', padding='same')(x)
x = UpSampling2D((2, 2))(x)
x = Conv2D(16, (3, 3), activation='relu')(x)
x = UpSampling2D((2, 2))(x)
decoded = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x)

autoencoder = Model(input_img, decoded)

モデルのsummaryは以下の通りです。

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_8 (InputLayer)         (None, 28, 28, 1)         0         
_________________________________________________________________
conv2d_43 (Conv2D)           (None, 28, 28, 16)        160       
_________________________________________________________________
max_pooling2d_19 (MaxPooling (None, 14, 14, 16)        0         
_________________________________________________________________
conv2d_44 (Conv2D)           (None, 14, 14, 8)         1160      
_________________________________________________________________
max_pooling2d_20 (MaxPooling (None, 7, 7, 8)           0         
_________________________________________________________________
conv2d_45 (Conv2D)           (None, 7, 7, 8)           584       
_________________________________________________________________
max_pooling2d_21 (MaxPooling (None, 4, 4, 8)           0         
_________________________________________________________________
conv2d_46 (Conv2D)           (None, 4, 4, 8)           584       
_________________________________________________________________
up_sampling2d_19 (UpSampling (None, 8, 8, 8)           0         
_________________________________________________________________
conv2d_47 (Conv2D)           (None, 8, 8, 8)           584       
_________________________________________________________________
up_sampling2d_20 (UpSampling (None, 16, 16, 8)         0         
_________________________________________________________________
conv2d_48 (Conv2D)           (None, 14, 14, 16)        1168      
_________________________________________________________________
up_sampling2d_21 (UpSampling (None, 28, 28, 16)        0         
_________________________________________________________________
conv2d_49 (Conv2D)           (None, 28, 28, 1)         145       
=================================================================
Total params: 4,385
Trainable params: 4,385
Non-trainable params: 0

学習

学習はこれまでと同じように行います。

autoencoder.fit(x_train, x_train,
                       nb_epoch=50,
                       batch_size=128,
                       shuffle=True,
                       validation_data=(x_test, x_test),)

以下が学習結果です。

CNNを使ったオートエンコーダもかなり鮮明に再現できていることが確認できました。

Denoising Autoencoder (DAE)

最後に試したのは、Denoising Autoencoder (DAE)と呼ばれるモデルです。

これは、ノイズ除去エンコーダとも呼ばれるもので、入力データに意図的にノイズを加えるモデルになっています。

ノイズが加わった入力からオリジナルの入力を復元しないといけないので、単純に値をコピーするわけにはいかなくなることで、精度の高い復元性を実現しようというようなモデルのようです。

前処理

まず、正規分布のノイズを加え、0から1の間の値を取るようにクリップします。

from keras.datasets import mnist
import numpy as np

(x_train, _), (x_test, _) = mnist.load_data()

x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28,28,1))
x_test = np.reshape(x_test, (len(x_test), 28,28,1))
print(x_train.shape)
print(x_test.shape)

noise_factor = 0.5
# 平均0、標準偏差1の正規分布

# (60000,1,28,28)の平均0、標準偏差1のデータにnoise_factorを足したものをx_trainに足してノイズを加える。

x_train_noisy = x_train + noise_factor * np.random.normal(loc=0., scale=1., size=x_train.shape)
x_test_noisy = x_test + noise_factor * np.random.normal(loc=0., scale=1., size=x_test.shape)


x_train_noisy = np.clip(x_train_noisy, 0., 1.)
x_test_noisy = np.clip(x_test_noisy, 0., 1.)

入力データの形状は以下の通りです。

x_train_noisy : (60000, 28, 28, 1)
x_test_noisy :  (10000, 28, 28, 1)

ノイズを加えた画像をチェック

ちゃんとノイズが加わっているかどうか入力画像をチェックしてみます。

import matplotlib.pyplot as plt

n = 10
plt.figure(figsize=(20, 2))
for i in range(n):
    ax = plt.subplot(1, n, i+1)
    plt.imshow(x_test_noisy[i].reshape(28, 28))
    plt.gray()
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
plt.show()

以下の通り、ノイズが加わった入力画像データになっていることが確認できました。

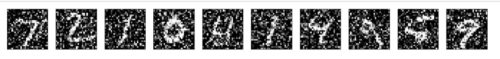
モデルの定義

モデルの定義自体は、先ほどのCNNモデルの場合と同じような構成になっています。

from keras.layers import Input, Dense, Conv2D, MaxPooling2D, UpSampling2D
from keras.models import Model

input_img = Input(shape=(28, 28, 1))

x = Conv2D(32, (3, 3), activation='relu', padding='same')(input_img)
x = MaxPooling2D((2, 2), padding='same')(x)
x = Conv2D(32, (3, 3), activation='relu', padding='same')(x)
encoded = MaxPooling2D((2, 2), padding='same')(x)

x = Conv2D(32, (3, 3), activation='relu', padding='same')(encoded)
x = UpSampling2D((2, 2))(x)
x = Conv2D(32, (3, 3), activation='relu', padding='same')(x)
x = UpSampling2D((2, 2))(x)
decoded = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x)

autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_4 (InputLayer)         (None, 28, 28, 1)         0         
_________________________________________________________________
conv2d_11 (Conv2D)           (None, 28, 28, 32)        320       
_________________________________________________________________
max_pooling2d_5 (MaxPooling2 (None, 14, 14, 32)        0         
_________________________________________________________________
conv2d_12 (Conv2D)           (None, 14, 14, 32)        9248      
_________________________________________________________________
max_pooling2d_6 (MaxPooling2 (None, 7, 7, 32)          0         
_________________________________________________________________
conv2d_13 (Conv2D)           (None, 7, 7, 32)          9248      
_________________________________________________________________
up_sampling2d_5 (UpSampling2 (None, 14, 14, 32)        0         
_________________________________________________________________
conv2d_14 (Conv2D)           (None, 14, 14, 32)        9248      
_________________________________________________________________
up_sampling2d_6 (UpSampling2 (None, 28, 28, 32)        0         
_________________________________________________________________
conv2d_15 (Conv2D)           (None, 28, 28, 1)         289       
=================================================================
Total params: 28,353
Trainable params: 28,353
Non-trainable params: 0

学習

ノイズを加えた画像を入力、ノイズのないオリジナルの画像をラベルとして学習させます。

autoencoder.fit(x_train, x_train,
                       nb_epoch=50,
                       batch_size=128,
                       shuffle=True,
                       validation_data=(x_test, x_test),)

以下が学習結果です。

かなり鮮明に復元できていることが確認できました。

まとめ

• オートエンコーダによる異常検知にも様々なモデルがある。

• Sparse Autoencoderは指定する正規化パラメータによって精度が大きくぶれる。
• エンコーダ、デコーダ層をディープ（複数階層）にすると精度向上が見込める。
• 画像系の異常検知にはCNNモデルのオートエンコーダを使ったほうがよさそう。
• Denoising Autoencoder (DAE）はノイズを加えることで精度の高い復元モデルの構築ができそう。

今回は、単純なMNISTデータを利用しただけなので何とも言えませんが、いろんなケースで検証することでどのようなデータの場合にどのオートエンコーダモデルが適しているかといった特徴、傾向を探っていきたいと思います。

以上、様々なオートエンコーダによる異常検知でした。

Django入門おすすめノート

note（ノート）

 

1 Pocket

Django WEBアプリ開発コース｜siny｜note

https://note.mu/shinya_hd/m/m7c72d8925919

以下のコースをまとめた割引プランです。 ・Djangoで毎月の出費を分析できる家計簿アプリをつくろう！【基礎編】 ￥980・Djangoで毎月の出費を分析できる家計簿アプリをつくろう！【応用編】 ￥500￥1,500相当のチュートリアルを、セット割で￥1,000で販売します。Djangoの環境構築からCRUD WEBアプリ開発+α Djangoの応用事例を学習したい人にお勧めです。ボリュームは約13万字ありますので、200～300ページ程度の技術書と同等のボリュームがあると思います。初心者用に図解を多く（約90枚）取り入れて、説明も多く掲載しています。