
目次
こんにちは。sinyです。
ディープラーニングにおいて、その精度向上には「データの前処理」が非常に重要になってくるわけですが、とある技術書を読んでいてデータ前処理として「入力データ値からその平均を引いて標準偏差で割って正規化します」と言った説明がでてきたのですが、これ以上の解説は特に書いてありませんでした。
「これって、統計学の基礎知識がない入門者が読んでもきっとわからないだろうな~」と思ったため、データ前処理に絡んで抑えておくべき統計学の基礎についてまとめてみました。
(認識違い等あればご指摘ください)
分散と標準偏差
データの分散
簡単に言うと、データの分散とは「データのばらつき具合」を示す数値です。
具体例を1つ挙げて説明しますね。
以下の表は、あるWEBシステムにおける1時間当たりの平均応答時間(単位はミリセカンド:ms)を表しています。
【表1-1】
| 時刻 | 10:00 | 11:00 | 12:00 | 13:00 | 14:00 | 15:00 | 16:00 | 17:00 | 18:00 |
|
応答時間(ms) |
3500 | 540 | 670 | 2400 | 200 | 230 | 240 | 130 | 100 |
この9個のデータの平均を計算すると「890 ms」になるので、このWEBシステムの平均応答時間はおおよそ1秒以内で結果が返ってくると判断できるわけです。
しかし、個々の時間帯をみていくと、平均応答時間は100~3500とばらついていることがわかりまよね。
では、このばらつきがどのくらいかをどうやって表現したらよいでしょうか?
その方法として、値から平均値を引くという考え方があります。
【表1-1】の各値から平均値「890」を引くと以下の表の値になります。
| 時刻 | 10:00 | 11:00 | 12:00 | 13:00 | 14:00 | 15:00 | 16:00 | 17:00 | 18:00 |
|
応答時間(ms) |
2610 | -350 | -220 | 1510 | -690 | -660 | -650 | -760 | -790 |
これは、各データが平均値からどの程度大きいか、または小さいかを表した数値になっています。
統計学ではこの数値を「偏差」と呼びます。
この偏差を見ることで、値が平均からどの方向にどの程度ずれているかを知ることができます。
ただ、最終的に知りたいのは全体の値のばらつきがどの程度かを表す1つの値です。
単純に上記で求まった偏差を足し合わせてしまうと、「+」と「-」の値があるため相殺されて正しい値が求められませんよね・・
そこで、統計学では以下のように「値の二乗」を足し合わせた合計値を求めて、値の個数で割るというアプローチをとります。
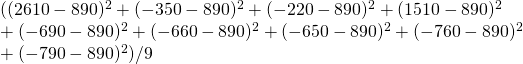
上記計算をすると「1311000」という値が求まります。
この値のことを統計学で「分散」と呼びます。
ただ、この分散の値では値が大きすぎて分散の具合がわかりづらいのと、値の単位が変わってしまっているという問題があるため、分散のルートをとって二乗平均を求めます。
![]()
= 1144.99となります。
このように偏差のルートをとることで単位がmsに揃い、値としても応答時間のブレの範囲と大体同じような感じになりますよね。
このようにして求めた値を統計学では「標準偏差」と呼びます。
標準偏差は「偏差」の2乗平均になっています。
標準偏差の意味を理解しよう
さて、上記で求めた標準偏差ですが、具体的にどういう意味かを理解しておくことは重要です。
今回のWEBシステムの例で言えば、平均応答時間が890msのシステムだが、1日で見るとおおよそ1144ms(1秒)のばらつきがあるということを示しています。
一般的な説明をすると、標準偏差は、平均値を基準にデータがどのくらいの広さで(+、ーの方向に)広がっているかを表す値といえます。
ディープラーニングにおけるデータ前処理の正規化
ディープラーニングの前処理では、精度を上げるためにデータの正規化というものを実施します。
正規化にもいろんなやり方があるのですが、今回は入力データの値を平均0、標準偏差が1となるようにデータを正規化するというパターンについて説明したいと思います。
そもそもなぜ正規化するのか?
端的にいうと、いろんな単位のデータを入力としてディープラーニングで学習させるより、共通の尺度で統一された値を入力データとして与えたほうが精度が良い学習モデルができるからです。
よくある例として、「身長」と「体重」から「性別」を判定する学習モデルを構築する場合、入力データに関して言うと、
身長→ ㎝(センチメートル)
体重→ kg (キログラム)
といったように入力数値の単位が異なります。
これをある共通の尺度のデータに変換してから学習モデルの入力データとして与えることで精度向上が期待できるわけです。
平均0、標準偏差1の値への正規化
よくある手法として、平均0、標準偏差1の値へ変換するという正規化の方法があります。
これは、「ある値から平均を引いて、標準偏差で割る」ことで求まります。
式で表すと以下のようになり、求まった値Zは「平均0、標準偏差1」の値に変換されます。
![]()
何をやっているかというと、
→入力値xから平均値を引いた値の標準偏差の値は変わりません。
②入力値(x)から平均値(μ)を引いた値の平均は0になります。
→入力値(x)の平均はμなので、xからμを引いた値の平均は「平均値ー平均値」=0になります。
③①で計算した値(x-μ)をσ(標準偏差)で割った値(Z)の標準偏差は1になります。
→(x-μ)の標準偏差はσなので、(x-μ)をσ(標準偏差)で割った値の標準偏差はσ/σ=1になります。
このようにして身長も、体重も Z = (x -μ) / σ という計算式に当てはめると平均0、標準偏差1のデータに変換されます。
言い換えると、以下のグラフのように平均が0、-1~1の範囲の正規分布に従うようなデータに変換できるというイメージです。
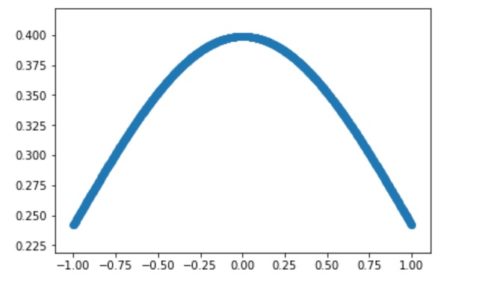
以上、ディープラーニングの前処理における正規化のお話でした。















