【ディープラーニング入門】ニューラルネットワークを理解しよう

こんにちは。sinyです。

【ディープラーニング入門】と題して、入門者向けにディープラーニングを理解するために必要な基本知識をシリーズとしてお届けして行きたいと思います。

というのも、そのうち社内でもディープラーニング勉強会なるものを実施していかなければいけない時期が来ると予想しているため、その元ネタにもなるので、改めて基礎知識について整理していきたいと思います。

まずは、初回ということで、ディープラーニングの基本原理の部分を理解していきましょう。

※この記事では、極力難しい言葉や数式を避けて、初心者が挫折しにくいように図解を交えて説明していきたいと思います。

まずはシンプルな予測機について考えてみよう

まずは、以下のような非常にシンプルな予測機を考えてみます。

コンピュータは、何らかの入力データを受け取り、処理（計算）した結果を出力します。
ディープラーニングのロジックも突き詰めていけば、この基本原理に基づいています。

では次に、もう少し具体的な事例で説明したいと思います。
例えば、人の体重（キログラム）を入力データに与えると、出力としてパウンド（Pound)の単位で数値を出力する場合を考えてみます。

上記のようにキログラム→パウンドに変換するロジックがわからなかったとします。
ただし、キログラムとパウンドの間には何かしらの関係性がありそうです。

そこで、パウンド＝キログラムｘ C という関係性が成り立つとします。（Cは定数）
また、キログラムとパウンドの関係としては、以下の値が正しいことがわかっています。

例	キログラム（kg)	パウンド（Pound）
①	0	0
②	50	110

定数Cとして何が正しいかはよくわかりませんので、とりあえず、上記例②のケースでC=3としてみます。
そうすると、パウンド＝キログラム（50）ｘ 3＝150となります。

しかし、このケースでは正解のパウンドは110であり、得られた解150とは40の誤差があります。

誤差が大きいので、次に定数Cの値を微調整してみます。
先ほどはC=3だったので今度はC=2に減らしてみます。

パウンド＝キログラム（50）ｘ 2＝100となります。

正解のパウンドは110であり、得られた解110とは10の誤差になります。
誤差が40→10に減少しました。

今度は定数C=1としてみます。

パウンド＝キログラム（50）ｘ 1＝50

正解のパウンドは110であり、得られた解50とは60の誤差になってしまいました。
誤差が先ほどよりだいぶ大きくなってしまいましたね。

C=３より2のほうが誤差が小さく、1にすると誤差が大きくなってしまうので、C=2付近で微調整すれば
より正解に近い値に近づきそうです。

そこで、C=1.5、1.75, 2.25としてみます。

パウンド＝キログラム（50）ｘ 1.5＝75         　110との誤差は35
パウンド＝キログラム（50）ｘ 1.75＝87.5    　110との誤差は22.5
パウンド＝キログラム（50）ｘ 2.25＝112.5  　110との誤差は2.5

こんな感じで出力結果と正解との誤差がより小さくなるように定数Cの値を調整していきます。
ポイントは、誤差が大きい間は調整幅も大きく、誤差が小さくなってきたら調整幅も小さくするという点です。

上記で行ってきた出力と正解の間の誤差を徐々に改善させるために定数Cの値を微調整していくというアプローチが、ディープラーニングでも用いられている基本的な考え方になっています。

ニューラルネットワークについて理解しよう

ニューラルネットワークとは、脳の神経回路をモデルにしたのもで、機械学習や、ディープラーニングのベースとなるモデルです。
まずは、基本となるニューラルネットワークの仕組みを理解することがディープラーニングの理解につながります。

以下が、ニューラルネットワークの基本形ですね。

 

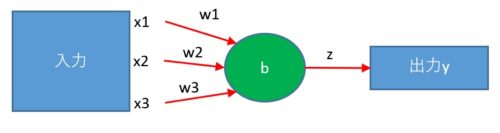
ニューラルネットワークといっても一番最初に説明した以下の図が基本になっています。

「何かの入力を受け取って、計算した結果を出力する」

ニューラルネットワークは、上記の基本形をちょっと発展させただけです。
入力が2つ以上だったり、計算の部分がちょっとだけ複雑になっていたり、出力する条件がちょっと追加になっているだけです。

では、以下のニューラルネットワークに仕組みについてざ～～と説明していきますね。

上図の場合は、入力データが３つ（x1,x2,x3）あります。
さらに入力データ毎に関連付けられる重みと呼ばれるパラメータ（w1,w2,w3)があります。
さらにバイオス「ｂ」と呼ばれるパラメータが１つあります。

ニューラルネットワークはこれらのパラメータを使って以下のような計算をします。

z = (x1・w1)＋(x2・w2)＋(x3・w3) + b

 

ニューラルネットワークについてざ～っと駆け足で説明しましたが、初めての人は「？？」という感じかもしれませんので、もう少し具体例に当てはめて説明しますね。

たとえば、「今週末に彼氏とデート！」なんていうケースで考えてみます。

こんなシーンを先ほどのニューラルネットワークに置き換えてみます。

各パラメータを以下のように定義します。

入力		重み		バイオス
パラメータ名	意味	パラメータ名	値
x1	デート場所までの距離 (キロメートル）	w1	0.2	-10
x2	天気 （晴れ=10、曇り=5、雨=1）	w2	0.5
x3	気温（度）	w3	0.7

※重みの値（0.2,0.5,0.7)は入力データに対してどのパラメータを一番重視するか？（値が大きいほど重視する）という意味合いと思ってもらえればよいと思います。
このようなパラメータを前提として、先ほどの計算式で得られる値「ｚ」に対して、

といった判断をするニューラルネットワークだとしましょう。

例えばデート当日の状態が以下だったとします。

この場合、以下の式に当てはめてｚを求めると・・・

z = (x1・w1)＋(x2・w2)＋(x3・w3) + b

z = (10・0.2)+(1・0.5)+(10・0.7) -10 = -1.5となります。
この場合は、zの値がマイナスなので「デートを断る！」という判断になります。

では、以下のケースではどうでしょうか？

z = (10*0.2)+(10*0.5)+(20*0.7) -10 = 21 
zの値が21＞０なのでプラスとなり、「デートに行く！」という判断になります。

ニューラルネットワークはこんな感じで、入力データｘに重み係数（w)を掛け合わせ、各値を足しこんだ後にバイオスと呼ばれるパラメータで調整した結果（ｚ）を求め、ｚがある閾値（今回の場合0より大きい）を超えた場合に出力する（デートに行くという行動をとる）、0以下なら出力しない（デートに行かない！）というような制御をするものになります。

いかがだったでしょうか？
なんとなくでも、ディープラーニングの基礎となるニューラルネットワークの仕組みについて理解していただけたら幸いです。