対数で掛け算を足し算に変換？　対数の２つのメリットを解説！

こんにちは。sinyです。

対数(log)はディープラーニングの根幹でもある逆誤差伝搬などでも利用されていますが、対数を扱うことによる２つのメリットについて簡単に紹介したいと思います。

対数とは？

対数をとると何がうれしいのか？

掛け算を足し算に変換できる。

logには以下のような公式がありますよね。

これは、掛け算を足し算に変換できるということです。

掛け算を足し算に変換できると何がうれしいか？

例えば、確率の計算で発生確率が0.05とか、0.0004とかいう数を何重にもかけ合わせていくと小数点以下が何十桁という扱いづらい数値になってしまいます。

そういった場合にlogをとって掛け算を足し算に変換できると、小数点以下が急増するのを避けることができるので計算がしやすくなるというメリットがあります。

他の具体例をあげると、以下のようなディープラーニングの誤差関数の導出式でlogをとっているのは計算コストを低くする、計算を単純化するためだと思われます。（どこかの書籍でもそのような説明がされていました）

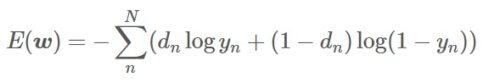
データの微妙な差をわかりやすく可視化できる。

対数をとることのメリットとして、グラフや表でデータを可視化する際に役に立つことが挙げられます。

例えば、以下のような商品別の合計金額を1つの表にすると、金額の大きなところだけが見えて、小さい部分（右側）が小さくなって比較しづらくなってしまいます。

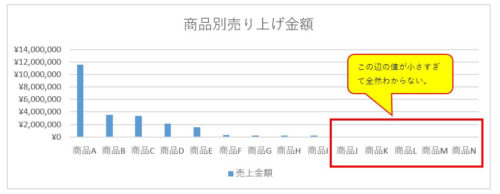
そこで、売上金額に対してlogをとってあげると、数値の大小関係を維持したまま、数値が大きいものは相対的に小さく、数値が小さいものは相対的に大きくなってバランスの良いグラフが出来上がります。

このように、logをとると売り上げ金額が小さい部分も数値の比較がしやすくなって便利ですね。

以上、対数を扱うことによる２つのメリットについてでした。