機械学習でアヤメデータ分類＆わかりやすく可視化してみよう

2019年1月19日 2019年1月19日

siny

1 アヤメと分類方法
2 K近傍法とは？
3 K近傍法を使ったアヤメデータの分類

こんにちは。sinyです。

この記事では、機械学習を使ったデータ分類について簡単な事例を交えて解説したいと思います。
今回は、よく機械学習の入門としても登場するアヤメデータ（irisデータとも言います）を使ってK近傍法と呼ばれるデータ分類手法を用いてアヤメデータを分類してみたいと思います。

アヤメと分類方法

今回利用するアヤメデータですが、アヤメは花の品種の１つで、3つの種類があります。

アヤメの種類

setosa（ヒオウギアヤメ）
Virginica
Versicolour(ブルーフラッグ)

また、アヤメの種類は以下の属性によって分類します。

アヤメ分類に利用する4つの属性

Sepal Length（がく片の長さ）
Sepal Width（がく片の幅）
Petal Length（花びらの長さ）
Petal Width（花びらの幅）

K近傍法とは？

K近傍法とは、未知のデータが与えられた場合に既存データのうち最も近くにあるK個のデータを使って多数決でデータを分類する、という大変シンプルなロジックです。

わかりやすく図にすると以下のようなイメージです。

既存のデータ点が、●と▲で、未知のデータが★です。

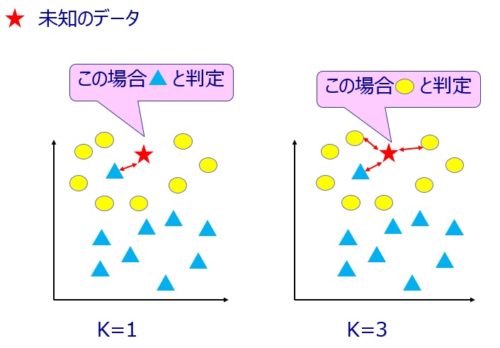
K=1とした場合（上図左側）は、新規データ★から最も近い既存データ▲に分類します。

続いてK=3とした場合(上図右側）は、新規データ★から最も近い既存データ３つ（●、●、▲）を選択し、その多数決をとって●に分類します。

多数決の結果、同数だった場合は重み(データ間の距離）によって判別します。

この手法は、学習モデルを作らないので非常にシンプルな学習ですが、データ量が多くなるについれて計算量が高くなるというデメリットがあります。

K近傍法を使ったアヤメデータの分類

今回は、PythonライブライのsklearnでK近傍法を使ってアヤメデータ分類してみます。

sklearnを使うとK近傍法のロジックを簡単に実装することができるので、入門者にもおすすめです。

　※この記事ではPytnon環境の構築や、JupyterNotebook等の使い方については省略しています。

　※本記事で記載しているコードについてはGITHUBにJupyterNotebook形式で公開しています。

まず最初に、必要なライブラリ、モジュールをインポートします。

from sklearn import datasets
import numpy as np
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.preprocessing import scale
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score

from sklearn import datasets

import numpy as np

from matplotlib.colors import ListedColormap

import matplotlib.pyplot as plt

import japanize_matplotlib

from sklearn.preprocessing import scale

from sklearn.model_selection import train_test_split

from sklearn.neighbors import KNeighborsClassifier

from sklearn.metrics import accuracy_score

モジュールの概要

from sklearn import datasets　
→データセットのインポート
import numpy as np　
→numpyのインポート
from matplotlib.colors import ListedColormap　
→グラフ描画でカラーマップを利用
import matplotlib.pyplot as plt　
→matplitolibをインポート
import japanize_matplotlib　
→matplotlibを日本語化
from sklearn.preprocessing import scale　
→前処理用のscaleメソッド
from sklearn.model_selection import train_test_split　
→訓練データ、テストデータに分類する機能
from sklearn.neighbors import KNeighborsClassifier　
→K近傍法の機能
from sklearn.metrics import accuracy_score　
→正解率の判定機能

続いて各種パラメータ値の設定を行い、アヤメデータ(IRIS)データをロードします。

# K近傍法の近傍数パラメータ k
neighbors = 5
# テストデータ分割のための乱数のシード（整数値）
random_seed = 1
#　テストデータの割合を指定
test_proportion = 0.3
# Iris データセットをロード 
iris = datasets.load_iris()
# 使用する特徴の次元を(Irisの場合は0,1,2,3から)2つ指定．d1とd2は異なる次元を指定すること
d1 = 0
d2 = 1

# すべての行のd1,d2列目の特徴量を取得
X = iris.data[:, [d1, d2]]
# クラスラベルを取得
y = iris.target
# z標準化（平均０、標準偏差1のデータに変換する）
X_std = scale(X)

# K近傍法の近傍数パラメータ k

neighbors = 5

# テストデータ分割のための乱数のシード（整数値）

random_seed = 1

#　テストデータの割合を指定

test_proportion = 0.3

# Iris データセットをロード

iris = datasets.load_iris()

# 使用する特徴の次元を(Irisの場合は0,1,2,3から)2つ指定．d1とd2は異なる次元を指定すること

d1 = 0

d2 = 1

# すべての行のd1,d2列目の特徴量を取得

X = iris.data[:, [d1, d2]]

# クラスラベルを取得

y = iris.target

# z標準化（平均０、標準偏差1のデータに変換する）

X_std = scale(X)

ソースの説明

neighbors = 5 　
　　　　→K近傍法のクラス数を指定します(データをいくつのデータ点で分類するか？）
random_seed = 1　
　　　　→　テストデータをランダムに分割するためのランダムシード
test_proportion = 0.3　　
　　　　→テストデータの割合を指定。(0.3=30%）
iris = datasets.load_iris()　　
　　　　→irisデータをsklearnからロードする。
d1 、d2　　
　　　　→d1,d2に特徴量を指定する。今回のirisデータの特徴量は0,1,2,3の４つ

　Sepal Length（がく片の長さ）→0
　Sepal Width（がく片の幅）→1
　Petal Length（花びらの長さ）→2
　Petal Width（花びらの幅）→3
X = iris.data[:, [d1, d2]]
　　　　→ d1,d2を使ってiris.dataから全行、d1,d2列の値だけを取得。
y = iris.target
　　　　→iris.tagetで正解データ(ラベル)を取得。
X_std = scale(X)
　　　　→入力データを平均０、標準偏差1のデータに正規化。

【補足】
入力データXの形状は(150, 2)になっていて、d1,d2で選択した入力データ(特徴量）のセットが150個あります。

#10件だけデータを表示
iris['data'][0:10]

array([[5.1, 3.5, 1.4, 0.2],
       [4.9, 3. , 1.4, 0.2],
       [4.7, 3.2, 1.3, 0.2],
       [4.6, 3.1, 1.5, 0.2],
       [5. , 3.6, 1.4, 0.2],
       [5.4, 3.9, 1.7, 0.4],
       [4.6, 3.4, 1.4, 0.3],
       [5. , 3.4, 1.5, 0.2],
       [4.4, 2.9, 1.4, 0.2],
       [4.9, 3.1, 1.5, 0.1]])

#10件だけデータを表示

iris['data'][0:10]

array([[5.1, 3.5, 1.4, 0.2],

[4.9, 3. , 1.4, 0.2],

[4.7, 3.2, 1.3, 0.2],

[4.6, 3.1, 1.5, 0.2],

[5. , 3.6, 1.4, 0.2],

[5.4, 3.9, 1.7, 0.4],

[4.6, 3.4, 1.4, 0.3],

[5. , 3.4, 1.5, 0.2],

[4.4, 2.9, 1.4, 0.2],

[4.9, 3.1, 1.5, 0.1]])

続いて、sklearnのtrain_test_splitメソッドを使って、入力データX_stdと、正解データｙを訓練データ（X_train,y_train)とテストデータ（X_test,y_test)に分割します。

# 変数test_proportionの割合をテストデータとし，変数random_seedを乱数生成器の状態に設定
X_train, X_test, y_train, y_test = train_test_split(X_std, y, 
                                    test_size = test_proportion, random_state = random_seed)

# 変数test_proportionの割合をテストデータとし，変数random_seedを乱数生成器の状態に設定

X_train, X_test, y_train, y_test = train_test_split(X_std, y,

test_size = test_proportion, random_state = random_seed)

次に、以下のコードでK近傍法のインスタンスを生成します。
sklearnを使うと複雑な計算式を実装しなくても1行でK近傍法のロジックを実装できます。

# クラスKNeighborsClassifierを使用してk近傍法のインスタンスを生成
knn = KNeighborsClassifier(n_neighbors=neighbors)

1 2	# クラスKNeighborsClassifierを使用してk近傍法のインスタンスを生成 knn = KNeighborsClassifier(n_neighbors=neighbors)

K近傍法のインスタンスを生成したら、fitメソッドに訓練用入力データ(X_train)と、訓練用正解ラベルデータ（y_train)を引数に指定して実行します。

# k近傍法のモデルを使って学習を実行
knn.fit(X_train, y_train)

1 2	# k近傍法のモデルを使って学習を実行 knn.fit(X_train, y_train)

学習が終わったら、分類結果を表示してみます。
正解率は、sklearnのaccuracy_scoreメソッドにaccurasy_score(正解ラベル,予測結果ラベル）の形で渡してあげると正解率を算出してくれます。

#分類結果
acc_train = accuracy_score(y_train, knn.predict(X_train))
acc_test = accuracy_score(y_test, knn.predict(X_test))
print('クラスタ数={},特徴選択={},{}'.format(neighbors, d1, d2))
print('train dataの正解率：{:.1f}%'.format(acc_train*100))
print('test dataの正解率：{:.1f}%'.format(acc_test*100))

#分類結果

acc_train = accuracy_score(y_train, knn.predict(X_train))

acc_test = accuracy_score(y_test, knn.predict(X_test))

print('クラスタ数={},特徴選択={},{}'.format(neighbors, d1, d2))

print('train dataの正解率：{:.1f}%'.format(acc_train*100))

print('test dataの正解率：{:.1f}%'.format(acc_test*100))

今回は、特徴量（d1,d2)として０[Sepal Length（がく片の長さ）]と1[Sepal Width（がく片の幅）]を選択してK近傍法によるクラス分類を実施してみましたが、結果は以下のようになりました。

クラスタ数=5,特徴選択=0,1
train dataの正解率：85.7%
test dataの正解率：68.9%

分類結果の可視化

最後にデータ分類結果を可視化して見ると、以下のようなクラス分けされた図になりました。

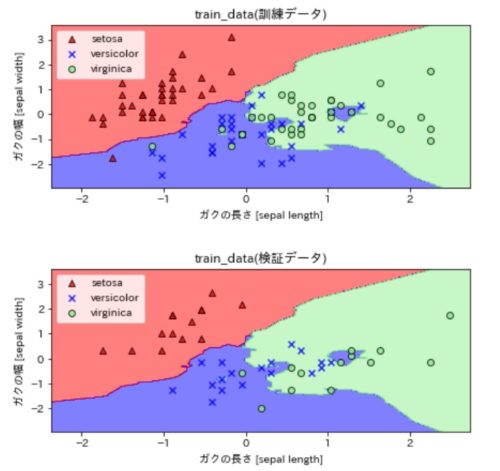
上図が、K近傍法を使って訓練データを分類した結果、下図がテストデータの分類結果になっています。
プロットされた点（▲、×、●）がデータセットの種類毎のアヤメデータです。
グラフの見方は、背景色に対してプロットされた色が違う部分が「誤分類」されているデータです。

K近傍法によってX軸とY軸(特徴量に選択した2つのデータ）を0.2刻みで入力データに与えた場合に、K近傍法で分類された結果（アヤメの3種類のいづれかに分類される）によってデータ点を赤、青、緑に塗りつぶしています。

0.2刻みと細かいので、見た目上は背景色として色付けされています。

下図では、test dataの正解率が68.9%ということもあり、誤分類されているデータがぽつぽつとあるのがわかると思います。

さてさて、上記のクラス分類図ですがmatplotlibを使うと描くことができるのですが、コードがちょっと長いのと1つ1つ説明するのは時間がかかってしまうので、この記事では割愛します。

ソースコードだけ掲載します。
(コメントも多めにつけてあるので読んでもらえれば何をやってるかは大体わかると思います）

def plot_decision_boundary():
    # X_trainの0番目の特徴量の最小値-0,5,最大値+0.5した値を取得
    x1_min, x1_max = X_train[:, 0].min() - 0.5, X_train[:, 0].max() + 0.5
    # X_trainの1番目の特徴量の最小値-0,5,最大値+0.5した値を取得
    x2_min, x2_max = X_train[:, 1].min() - 0.5, X_train[:, 1].max() + 0.5
    #特徴量１，２を最小～最大の間で0.02刻みのデータ点を生成し、meshgridでグリッドデータを生成
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.02),
                           np.arange(x2_min, x2_max, 0.02))
                       
    """k近傍法の予測結果を取得
       ravel()で1次元に変換。(328, 269)→ (2,88232)
       predict(予測データ)
      .Tで(2, 88232)　→(88232, 2)に変換(入力データ X_train同じ形状(105,2)へ変換している)
      つまり、0.02刻みで発生させた特徴量データ点xx1,xx2を入力にしてpredictさせた結果をZに格納している。
    """
    Z = knn.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    #マーカー種類の定義
    markers = ('^', 'x', 'o', 's', 'v')
    #色の設定
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    #colorsリストから、出力ｙの種類の数分、色の情報を持ったオブジェクトを生成する。
    cmap = ListedColormap(colors[:len(np.unique(y))])
    

    #プロット図のサイズを指定
    plt.figure(figsize=(7, 7))
    #図の間隔を調整
    plt.subplots_adjust(wspace=0.5, hspace=0.5)
    # plt.subplot(行数, 列数, 何番目のプロットか)を指定 
    plt.subplot(2,1,1)
    
    # meshgrid で作った xx1 と xx2、そして高さに相当する予測結果Z を contour に渡す
    # contourf(X軸の配列、Y軸の配列、高さZ)の形式が基本系
    # こうすると、Z（予測結果）の種類毎にcmapの色でプロットされる。
    plt.contourf(xx1, xx2, Z, alpha=0.5, cmap=cmap)
    # x軸の範囲を特徴量1の最小～最大に指定
    plt.xlim(xx1.min(), xx1.max())
    # y軸の範囲を特徴量2の最小～最大に指定
    plt.ylim(xx2.min(), xx2.max())

    
    """plt.scatter(X,Y)で散布図を描画
       clは今回は０，１，２のラベル
       X_train[y_train == cl, 0]
         → y_trainが特定のラベルの行の0列目のX_trainデータだけを抽出している。
        y_train = 1などとすると以下のようにTrue,Falseのアレイ要素が返ってくるので
        そのTrue,False配列をX_trainのｘ軸のスライスに指定すると、該当ラベルだけの行のX_trainを取得できる。
        array([ True, False, False, False, False, False,  True,  True,  True,
              False,  True,  True,  True)]
    """
    #凡例ラベルの格納リスト
    legend =[]
    for index, color in enumerate(np.unique(y_train)):
        p = plt.scatter(x=X_train[y_train == color, 0], y=X_train[y_train == color, 1],
                    alpha=0.8, c=cmap(index),marker=markers[index], label=color, edgecolors='black')
        legend.append(p)     

    #凡例（正解ラベル情報）の表示
    plt.legend(legend,iris.target_names)
    plt.xlabel('ガクの長さ [sepal length]')
    plt.ylabel('ガクの幅 [sepal width]')
    plt.title('train_data(訓練データ)')
    
    plt.subplot(2,1,2)
    plt.contourf(xx1, xx2, Z, alpha=0.5, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())
    
    #凡例ラベルの格納リスト
    legend =[]
    for index, color in enumerate(np.unique(y_test)):
        p= plt.scatter(x=X_test[y_test == color, 0], y=X_test[y_test == color, 1],
                        alpha=0.8, c=cmap(index),marker=markers[index], label=color, edgecolors='black')
        legend.append(p)        
        
    #凡例（正解ラベル情報）の表示
    plt.legend(legend,iris.target_names)
    plt.xlabel('ガクの長さ [sepal length]')
    plt.ylabel('ガクの幅 [sepal width]')
    plt.title('train_data(検証データ)')
    plt.show()

def plot_decision_boundary():

# X_trainの0番目の特徴量の最小値-0,5,最大値+0.5した値を取得

x1_min, x1_max = X_train[:, 0].min() - 0.5, X_train[:, 0].max() + 0.5

# X_trainの1番目の特徴量の最小値-0,5,最大値+0.5した値を取得

x2_min, x2_max = X_train[:, 1].min() - 0.5, X_train[:, 1].max() + 0.5

#特徴量１，２を最小～最大の間で0.02刻みのデータ点を生成し、meshgridでグリッドデータを生成

xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.02),

np.arange(x2_min, x2_max, 0.02))

"""k近傍法の予測結果を取得

ravel()で1次元に変換。(328, 269)→ (2,88232)

predict(予測データ)

.Tで(2, 88232)　→(88232, 2)に変換(入力データ X_train同じ形状(105,2)へ変換している)

つまり、0.02刻みで発生させた特徴量データ点xx1,xx2を入力にしてpredictさせた結果をZに格納している。

"""

Z = knn.predict(np.array([xx1.ravel(), xx2.ravel()]).T)

Z = Z.reshape(xx1.shape)

#マーカー種類の定義

markers = ('^', 'x', 'o', 's', 'v')

#色の設定

colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')

#colorsリストから、出力ｙの種類の数分、色の情報を持ったオブジェクトを生成する。

cmap = ListedColormap(colors[:len(np.unique(y))])

#プロット図のサイズを指定

plt.figure(figsize=(7, 7))

#図の間隔を調整

plt.subplots_adjust(wspace=0.5, hspace=0.5)

# plt.subplot(行数, 列数, 何番目のプロットか)を指定

plt.subplot(2,1,1)

# meshgrid で作った xx1 と xx2、そして高さに相当する予測結果Z を contour に渡す

# contourf(X軸の配列、Y軸の配列、高さZ)の形式が基本系

# こうすると、Z（予測結果）の種類毎にcmapの色でプロットされる。

plt.contourf(xx1, xx2, Z, alpha=0.5, cmap=cmap)

# x軸の範囲を特徴量1の最小～最大に指定

plt.xlim(xx1.min(), xx1.max())

# y軸の範囲を特徴量2の最小～最大に指定

plt.ylim(xx2.min(), xx2.max())

"""plt.scatter(X,Y)で散布図を描画

clは今回は０，１，２のラベル

X_train[y_train == cl, 0]

→ y_trainが特定のラベルの行の0列目のX_trainデータだけを抽出している。

y_train = 1などとすると以下のようにTrue,Falseのアレイ要素が返ってくるので

そのTrue,False配列をX_trainのｘ軸のスライスに指定すると、該当ラベルだけの行のX_trainを取得できる。

array([ True, False, False, False, False, False, True, True, True,

False, True, True, True)]

"""

#凡例ラベルの格納リスト

legend =[]

for index, color in enumerate(np.unique(y_train)):

p = plt.scatter(x=X_train[y_train == color, 0], y=X_train[y_train == color, 1],

alpha=0.8, c=cmap(index),marker=markers[index], label=color, edgecolors='black')

legend.append(p)

#凡例（正解ラベル情報）の表示

plt.legend(legend,iris.target_names)

plt.xlabel('ガクの長さ [sepal length]')

plt.ylabel('ガクの幅 [sepal width]')

plt.title('train_data(訓練データ)')

plt.subplot(2,1,2)

plt.contourf(xx1, xx2, Z, alpha=0.5, cmap=cmap)

plt.xlim(xx1.min(), xx1.max())

plt.ylim(xx2.min(), xx2.max())

#凡例ラベルの格納リスト

legend =[]

for index, color in enumerate(np.unique(y_test)):

p= plt.scatter(x=X_test[y_test == color, 0], y=X_test[y_test == color, 1],

alpha=0.8, c=cmap(index),marker=markers[index], label=color, edgecolors='black')

legend.append(p)

#凡例（正解ラベル情報）の表示

plt.legend(legend,iris.target_names)

plt.xlabel('ガクの長さ [sepal length]')

plt.ylabel('ガクの幅 [sepal width]')

plt.title('train_data(検証データ)')

plt.show()

最適な近傍点を分析する

つづいて、K近傍法法で指定するK近傍法パラメータK（neighbors）の値を動的に変化させて、正解率をプロットしてみます。
※特徴量は0，1を選択したまま

accurate = []
k_range = []
 
for k in range(1, 90):
    knn = KNeighborsClassifier(n_neighbors=k)
    knn.fit(X_train, y_train)
    score  = accuracy_score(y_test, knn.predict(X_test))
    accurate.append(score)
    k_range.append(k)
    
# X軸に近傍点
# Y軸に評価値
plt.plot(k_range, accurate)
plt.grid()

accurate = []

k_range = []

for k in range(1, 90):

knn = KNeighborsClassifier(n_neighbors=k)

knn.fit(X_train, y_train)

score = accuracy_score(y_test, knn.predict(X_test))

accurate.append(score)

k_range.append(k)

# X軸に近傍点

# Y軸に評価値

plt.plot(k_range, accurate)

plt.grid()

結果は以下のようになりました。
K=10前後が一番結果がよく、それ以上やみくもに増やしても効果がないことがわかりますね。

特徴量を変えてみる

今度は分類に使う特徴量を変えてみます。

これまでは、特徴量としてがく片の長さ（＝０列目のデータ）とがく片の幅（＝1列目のデータ)を使っていましたが、花びらの長さと幅を使ってK近傍法による分類を実施してみます。

利用する特徴量は以下のソースコードで指定しているので、d1,d2の値を0,1→2,3に変更するだけでOKです。

# 使用する特徴の次元を(Irisの場合は0,1,2,3から)2つ指定．d1とd2は異なる次元を指定すること
d1 = 2
d2 = 3

# 使用する特徴の次元を(Irisの場合は0,1,2,3から)2つ指定．d1とd2は異なる次元を指定すること

d1 = 2

d2 = 3

neighbors の値は5のままで実行してみます。

結果は、以下の通り正解率が大幅に上昇しました。

選択する特徴量によって分類精度が大きく変わるということですね。
機械学習では、選択する特徴量によって精度が大きく変動する点がポイントになりそう。

選択する特徴量によって分類精度が大きく変わるということですね。
機械学習では、このように選択する特徴量によって精度が大きく変動する点がポイントになりそうですね。

クラスタ数=5
特徴選択=2,3
train dataの正解率：98.1%
test dataの正解率：95.6%

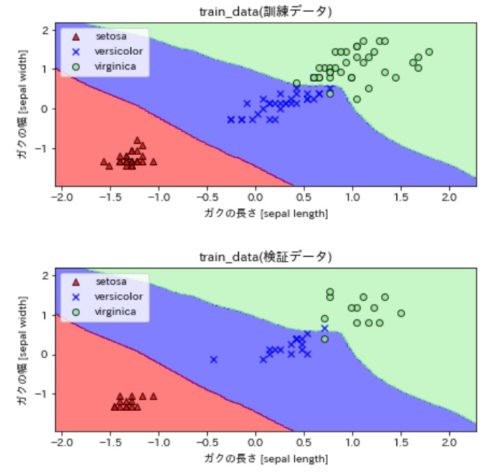
特徴量を2，3に変更した場合の分類結果を可視化したのが下図です(ラベルはガクの長さと幅のまま修正してません）。

だいぶきれいに分離されているのが図からもわかりますね！

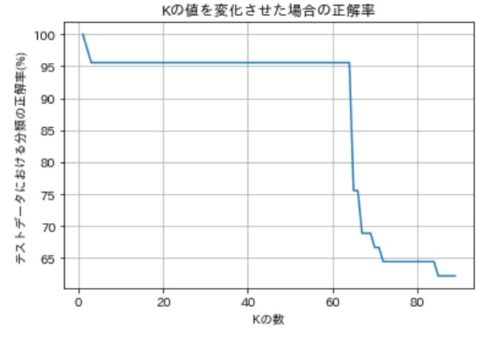
ついでにこの場合にKの値を変動させたグラフもプロットしてみました。
最適なKは3前後くらいのようですね。
今回は、K＝60過ぎまで一定で、それ以上になるとガクンと精度が落ちることもわかりました。

以上、K近傍法によるアヤメデータ分類でした。

機械学習に興味を持っている方は、本記事を参考にぜひデータ分類にチャレンジしてみてください！

この記事を書いた人

siny

現在の仕事は社内SEのお仕事です。趣味でDjango,Python,機械学習、ディープラーニングなどをやってます。